
La inestabilidad inherente en el eje de longitud media o $ \ prod_2 $ como se muestra arriba se analiza en detalle en Marsden y Ratiu, que es donde la imagen es desde.
La órbita homoclínica inestable que conecta los dos puntos inestables tiene características interesantes. No solo son interesantes debido a las soluciones caóticas a través del método de Poincaré-Melnikov que se pueden obtener en varios sistemas perturbados (ref), sino que la órbita en sí es interesante ya que un cuerpo rígido arrojado sobre su eje medio sufrirá un medio giro interesante (e inesperado) cuando se alcanza el punto de silla opuesto a pesar de que el eje de rotación ha vuelto a donde estaba.
El medio giro interesante se muestra mejor en el " efecto Dzhanibekov" y también se puede ver en el " teorema de la raqueta de tenis".
Para aquellos que no entienden por qué el punto de silla a lo largo del eje de longitud media $ \ prod_2 $ en la imagen de arriba es inestable, considere la siguiente imagen:
 Fuente de la imagen
Fuente de la imagen
Los tres ejes que describe son comparables respectivamente con:
- ~ una barra / eje
- ~ un Fly- rueda
- ~ una hélice
¿Qué es la estabilidad y por qué dos ejes son estables mientras que el tercero es inestable?
La estabilidad se refiere a una oscilación "estable", que debe ser armónica como una masa en un resorte. Hay una fuerza restauradora proporcional al desplazamiento.
$$ F = -k * x = m * a = m * \ frac {d ^ 2x} {dt ^ 2} ~~~~~~~~~~~~~~~ ~~~~ \ text {(1)} $$ Para situaciones angulares la situación se vuelve mucho más complicada ya que el par es normal al plano de rotación. $$ \ tau = - \ kappa \ theta = I * \ dot {\ omega} = I * \ frac {d ^ 2 \ theta} {dt ^ 2} ~~~~~~~~~~~~~~ ~~~~~~ \ text {(2)} $$
Cuando hay una fuerza fuera del eje alrededor de un eje estable, hay dos componentes de torque: uno a lo largo del eje primario que siempre causará una rotación lineal y un segundo perpendicular al eje (aproximadamente 1 o ambos de los otros ejes), que en ausencia de la rotación primaria (o con una distribución de masa uniforme) también causaría una rotación lineal. Entonces siempre hay dos pares de torsión; el principal grande, el segundo pequeño. Con oscilaciones armónicas estables, al igual que con ejes de rotación estables, existe una fuerza de restauración proporcional al desplazamiento. Richard Feynman ha realizado un trabajo fascinante para describir una placa que se tambalea, que se tambaleará dos veces más de lo que gira.
Sea $ \ hat {x} _1 $, $ \ hat {x} _2 $ y $ \ hat {x} _3 $ deben ser ejes a lo largo de los ejes más largo, medio y más corto del prisma rectangular, respectivamente. Durante la rotación estable (que ocurre cuando la rotación primaria es de aproximadamente $ \ hat {x} _1 $ y $ \ hat {x} _3 $), los ejes secundarios trazan círculos como lo describe Feynman.
Realizar un análisis de un prisma rectangular de acuerdo con el método descrito por Feynman ciertamente mostrará que la rotación alrededor de $ \ hat {x} _2 $ crea una espiral en lugar de un círculo.
Se produce la espiral
Imagínese cómo un disco que gira sobre su eje es muy estable: la diferencia entre los momentos de inercia sobre los otros dos ejes es cero: es muy estable. Ahora reemplace el disco "O" con una estructura en forma de "X" que gira a lo largo de un eje normal al plano de la X. La rotación es estable nuevamente por la misma razón. Corta dos brazos de la X en lados opuestos y la barra recta continúa girando en oscilaciones estables. Ahora agregue un cable a lo largo del eje de rotación pero que sobresalga de un solo lado de la varilla. De repente, aparece el efecto Dzhanibekov, que es inestable al igual que agregar ancho a la varilla a lo largo del eje de rotación para formar una forma comparable a un prisma rectangular. En el caso del cable, sigue siendo desconcertante, pero creo que proporciona una idea de la naturaleza del problema. Especialmente teniendo en cuenta que un trompo (disco giratorio con un cable que lo atraviesa asimétricamente) es muy estable, al igual que un trompo en forma de X ... mientras que un trompo en forma de hélice ni siquiera es un trompo en realidad. Así que tome una peonza en forma de O que gire en gravedad cero y haga volar al azar trozos del disco en forma de casi semicírculo para que se convierta en una hélice. Ahora, el momento de inercia alrededor del eje de la "pala" de la hélice giratoria (el eje de longitud más larga) se reduce en gran medida mientras que al mismo tiempo se reduce drásticamente la fuerza giroscópica. Tiene sentido que este eje (el más largo) se convierta en "un eje de rotación libre" en un grado u otro ... con las fuerzas giroscópicas o centrífugas de la "cuchilla" giratoria que se suman y luego se restan del eje a medida que avanza. se mueve hacia adelante y hacia atrás en el efecto Dzhanibekov. La diferencia entre la longitud del eje de longitud media $ \ prod_2 $ y el eje más corto $ \ prod_1 $ cumple la misma función que el eje del objeto similar a una hélice en el efecto Dzhanibekov: específicamente, da y toma energía centrípeta del eje de rotación primario $ \ prod_2 $ representado por el punto de silla.
Además, observe cómo una peonza, cuando se desacelera, comienza a precesar en círculos cada vez más grandes hasta que se cae. ¿Es eso una mera precesión giroscópica? ¿O es el primer signo de oscilación inestable comparable a la traza en espiral del eje en el efecto Dzhanibekov? Yo especularía que es un poco de ambos: la parte superior probablemente no sea un disco perfecto y una vez que el bamboleo comience, la precesión giroscópica probablemente se agregue.
Debo añadir que una parte superior en forma de Y (60 grados de separación) tiene algunas propiedades particularmente fascinantes, ya que tiene similitudes tanto con una caja como con una hélice, pero sigue siendo una parte superior porque la simetría radial permite que las fuerzas giroscópicas se estabilicen. el eje de longitud media. Como señaló Ben Crowell en los comentarios, este efecto se explica con hermosos detalles intuitivos aquí en la sección 4.3.3, cuyo enlace directo al pdf es aquí. Copié la explicación allí de la siguiente manera:
Para un objeto asimétrico típico, el vector de momento angular y el vector de velocidad angular no necesitan ser paralelos. Es decir, solo para un cuerpo que posee simetría con respecto al eje de rotación es cierto que $ L = I \ omega $ (el equivalente rotacional de $ p = mv $) para algún escalar I ... . (derivación elegante de :)
$$ K = \ frac 12 L \ cdot \ omega $$ .... Analicemos el problema del zapato giratorio que planteé al principio del capítulo. Los tres ejes de rotación (comparables a un prisma rectangular) a los que se hace referencia allí son aproximadamente los ejes principales del zapato. Mientras el zapato está en el aire, no actúan pares externos sobre él, por lo que su vector de momento angular debe ser constante. Sin embargo, eso está en el marco de referencia de la sala. El marco del eje principal está sujeto al zapato y cae locamente con él. En el marco del eje principal, la energía cinética y la magnitud del momento angular permanecen constantes, pero la dirección real del momento angular no necesita permanecer fija (como se vio en el caso de la rotación que inicialmente fue sobre el eje de longitud intermedia) . La constante $ | L | $ da $$ {L_x} ^ 2 + {L_y} ^ 2 + {L_z} ^ 2 = constante $$ En el marco del eje principal, es fácil resolver las componentes de $ \ omega $ en términos de los componentes de L, por lo que eliminamos $ \ omega $ de la expresión $ 2K = L \ cdot \ omega $, dando $$ \ frac {1} {I_xx} {L_x} ^ 2 + \ frac {1} {I_yy } {L_y} ^ 2 + \ frac {1} {I_zz} {L_z} ^ 2 = constante \ # 2 $$
La primera ecuación es la ecuación de una esfera en el espacio tridimensional ocupado por el vector de momento angular, mientras que el segundo es la ecuación de un elipsoide: 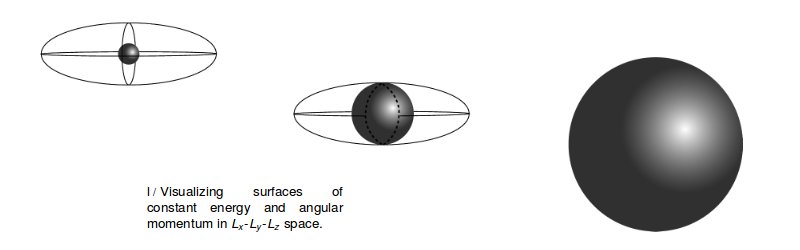
La cifra superior corresponde al caso de rotación sobre el eje más corto, que tiene el elemento de mayor momento de inercia. La intersección de las dos superficies consta solo de los dos puntos en la parte delantera y trasera de la esfera. El momento angular se limita a uno de estos puntos, y no puede cambiar su dirección, es decir, su orientación con respecto al sistema de eje principal, que es otra forma de decir que el zapato no puede cambiar su orientación con respecto al eje principal. vector de momento angular. En la figura inferior, el zapato gira sobre el eje más largo. Ahora, el vector de momento angular está atrapado en uno de los dos puntos a la derecha oa la izquierda. Sin embargo, en el caso de la rotación alrededor del eje con el elemento intermedio de momento de inercia, la intersección de la esfera y el elipsoide no es solo un par de puntos aislados, sino la curva que se muestra con la línea discontinua. La orientación relativa del zapato y el vector de momento angular pueden cambiar y cambiarán.
Una aplicación del tensor de momento de inercia es para videojuegos que simulan carreras de coches o aviones volando ....
Un ejemplo más exótico tiene que ver con la física nuclear. Aunque probablemente haya visualizado los núcleos atómicos como nada más que puntos sin rasgos distintivos, o quizás esferas diminutas, a menudo son elipsoides con un eje largo y dos más cortos e iguales. Aunque un núcleo en rotación normalmente se deshace de su momento angular a través de la emisión de rayos gamma en un período de tiempo del orden de picosegundos, puede suceder que un núcleo deformado entre en un estado en el que un gran momento angular se encuentre a lo largo de su eje largo, que es un modo de rotación muy estable. ¡Estos estados pueden vivir segundos o incluso años! (Hay más en la historia, este es el tema sobre el que escribí mi tesis de doctorado, pero la información básica se aplica a pesar de que el tratamiento completo requiere una mecánica cuántica elegante).

Nuestro análisis ha asumido hasta ahora que la energía cinética de la energía de rotación no se puede convertir en otras formas de energía como calor, sonido o vibración. Cuando esta suposición falla, entonces la rotación sobre el eje de menor momento de inercia se vuelve inestable y eventualmente se convertirá en rotación sobre el eje cuyo momento de inercia es mayor. Esto sucedió con el primer satélite artificial de los EE. UU., Explorer i, lanzado en 1958. Tenga en cuenta las largas antenas flexibles, que tendían a disipar la energía cinética en vibración. Había sido diseñado para girar sobre su eje de mínimo momento de inercia, pero casi de inmediato, tan pronto como estuvo en el espacio, comenzó a girar de un extremo a otro. No obstante, pudo llevar a cabo su misión científica, que no dependía de poder mantener una orientación estable, y descubrió los cinturones de radiación de Van Allen.
Una pregunta relacionada aquí sobre Physics.SE
Una pregunta relacionada sobre MathOverflow
Imagen tomada de Marsden y Ratiu.