Un suéter súper grueso probablemente no sea el camino a seguir; es mejor que te envuelvas en papel de aluminio.
El cuerpo pierde calor a través de varios mecanismos:
- Durante la conducción , su cuerpo transfiere calor al aire circundante que está en contacto con su piel. Esto eleva la temperatura del aire, lo que (si el aire está quieto) disminuye la tasa de pérdida de calor.
- Si el aire se mueve, la brisa se lleva esa energía y usted está en contacto con aire fresco básicamente todo el tiempo. Esto es convección .
- La evaporación ocurre cuando la humedad de la piel pasa del líquido a la fase gaseosa, llevándose energía junto con ella. Esto depende de la humedad relativa del aire; consulte temperatura de bulbo húmedo para obtener más información.
- En todo momento, su cuerpo emite radiación (principalmente en el infrarrojo), con una pérdida total de energía dada por $ P = \ epsilon A \ sigma T ^ 4 $ . Aquí,
- $ \ epsilon $ es la emisividad de tu cuerpo, ( $ \ epsilon \ approx 0.95 $ Si
estás desnudo)
- $ A $ es el "área de radiación efectiva" de su cuerpo
( $ A \ approx 0.7 (2 \ text {m} ^ 2) \ approx1.4 \ text {m} ^ 2 $ )
- $ \ sigma $ es el
Constante de Stefan-Boltzmann $ \ sigma = 5.67 \ times 10 ^ {- 8}
\ frac {\ text {W}} {\ text {m} ^ 2 \ text {K} ^ 4} $
- $ T $ es la temperatura absoluta de su cuerpo en Kelvin.
(Tenga en cuenta que su cuerpo emite radiación, pero también la recibe , y la cantidad depende de su entorno de radiación particular).
De estos cuatro mecanismos, los dos primeros son irrelevantes para tu pregunta porque estás en un vacío. La evaporación definitivamente ocurrirá, especialmente alrededor de la nariz, la boca y los ojos, pero creo que el modo principal de pérdida de calor aquí será la radiación, así que centrémonos en eso.
Su cuerpo genera calor en todo momento a través de su metabolismo y de la fricción interna. Si se relaja en condiciones cómodas, está produciendo aproximadamente 100 W, pero este número aumenta si comienza a hacer ejercicio. En particular, cuando su cuerpo se enfría, su cerebro activa el reflejo de escalofríos, lo que puede hacer que la producción de energía de su cuerpo salte a 200-300 W.
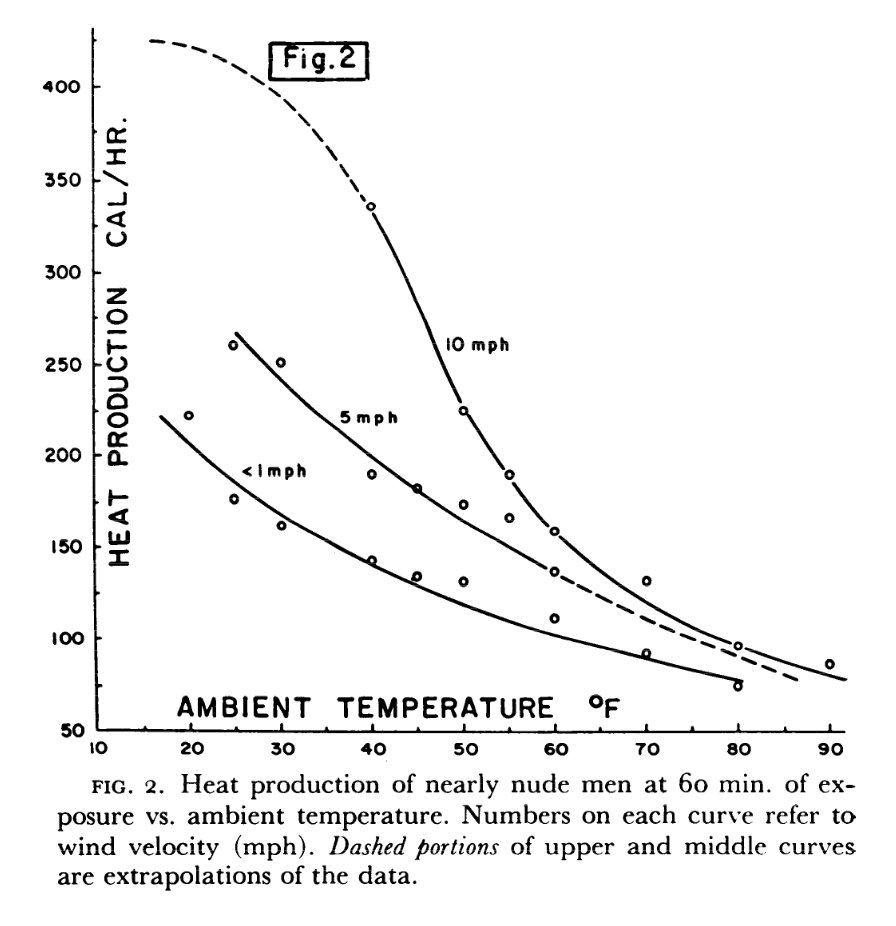
Fuente (tenga en cuenta que $ 1 \ text {Cal / hr} \ approx 1 \ text {W} $ ).
Ignorando por un momento el efecto de la ropa, entonces su temperatura corporal de equilibrio puede estimarse aproximadamente equiparando la energía generada por sus procesos metabólicos (y posiblemente el movimiento) con la pérdida de energía a través de la radiación, asumiendo que no está absorbiendo la radiación de en cualquier otro lugar. Supongo que el cuerpo está a una temperatura uniforme aquí. Este no sería el caso: el centro de su cuerpo estaría más caliente y luego se formaría un gradiente en su piel, pero esto puede descuidarse porque el gradiente no sería muy extremo.
En este modelo simplificado, esta es la temperatura corporal de equilibrio resultante en función de la emisividad, asumiendo primero 100 W y luego 300 W de potencia generada.
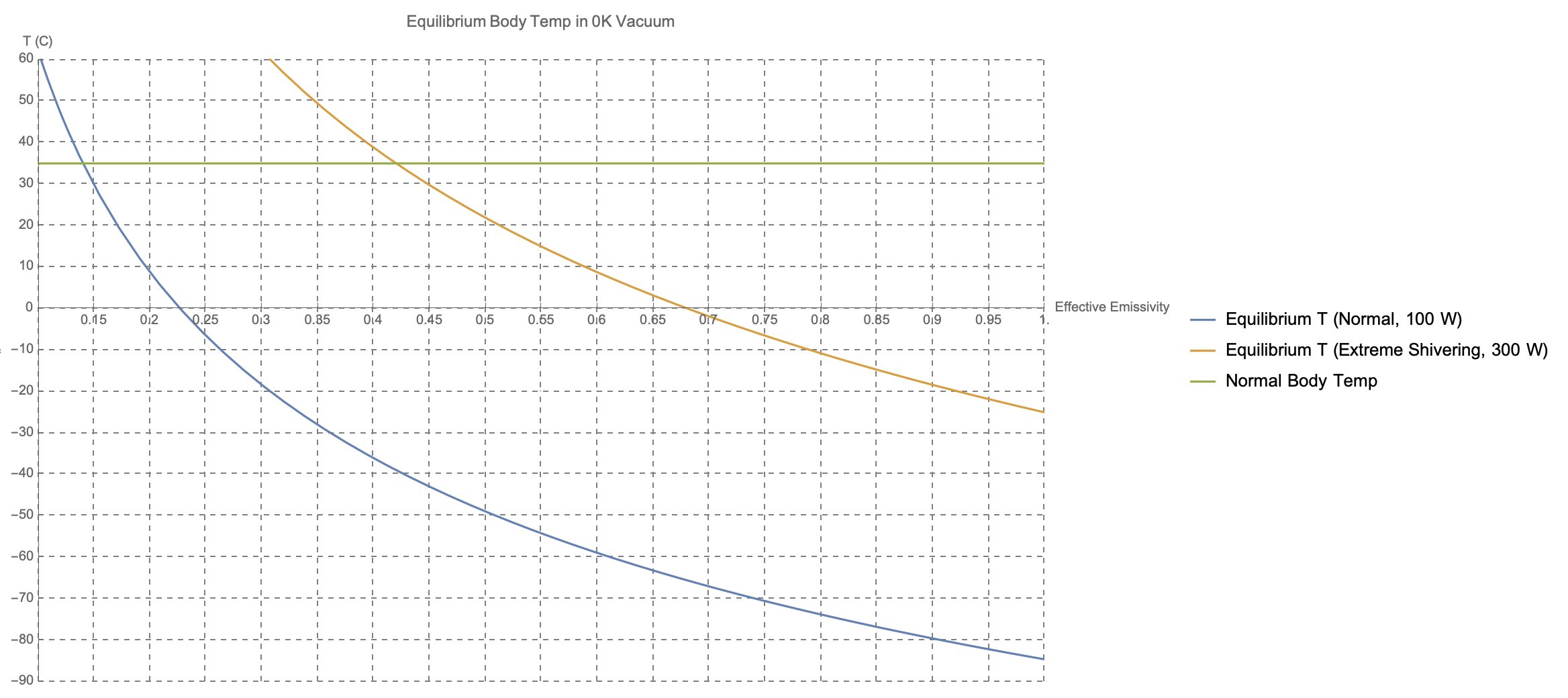
Como puede ver, la situación es bastante desoladora si se enfrenta al vacío desnudo. Su temperatura central no puede caer muy por debajo de sus 37 C normales antes de entrar en un estado hipotérmico; incluso temblando ferozmente , esto requiere una emisividad de algo como $ 0.425 $ , muy por debajo del valor típico de su cuerpo de $ 0.95 $ .
Aquí es donde entra la ropa. Los textiles tienen una emisividad algo más baja que los humanos desnudos. La emisividad superficial de la lana es de aproximadamente 0,74 y la mayoría de los textiles se encuentran en ese rango o más, lo que significa que la superficie de la prenda aún se equilibraría por debajo de 0 C.
Sin embargo, la conductividad térmica de la lana es solo de $ 0.03 \ frac {\ text {W}} {\ text {m K}} $ . Para una prenda de grosor $ t $ que cubra todo el cuerpo, el gradiente de temperatura desde la superficie de su cuerpo hasta la superficie de la prenda sería
$$ \ frac {\ Delta T} {t} = - \ frac {100 \ text {W}} {2 \ text {m} ^ 2 \ cdot 0.03 \ texto {W / mK}} \ approx 1670 \ frac {\ text {K}} {\ text m} $$
A partir de la temperatura del exterior de la prenda, esto nos permite rastrear y encontrar la temperatura corporal correspondiente en función del grosor. He realizado el cálculo para lana y algodón, con los resultados que se muestran a continuación.
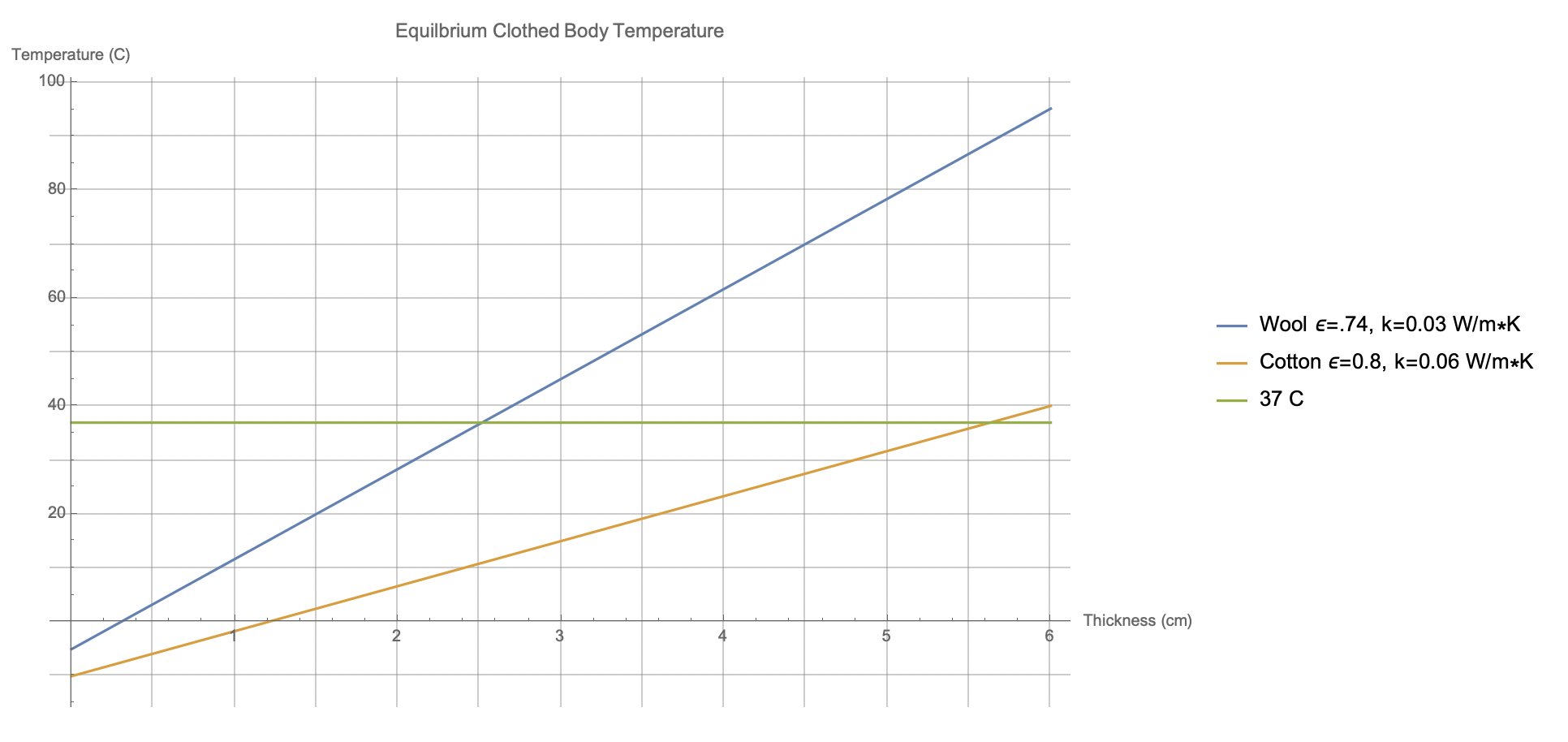
La superficie de un suéter de lana se equilibraría a aproximadamente -5 C, lo que correspondería a una temperatura corporal de 37 C si el grosor del suéter fuera solo de unos 3 cm. Eso es grueso, ciertamente, pero no absurdamente. Para un suéter de algodón, que tendría tanto una emisividad más alta como una conductividad térmica más alta, la superficie se equilibraría alrededor de -10 C y necesitaría un grosor cercano a los 6 cm para mantenerse caliente.
Por otro lado, podría considerar envolverse en una capa de material de emisividad extremadamente baja, y eso sería mucho más efectivo. La plata pulida, por ejemplo, tiene una emisividad de solo $ 0.02 $ , lo que sería problemático en la dirección incorrecta. Para irradiar 100 W / m $ ^ 2 $ , nuestra capa debería tener una temperatura superficial de unos 60 C, lo que nos asaría vivos. El punto óptimo, en el que nuestro cuerpo se equilibraría a 37 ° C, parece corresponder a una emisividad de aproximadamente $ 0.15 $ . Según esta tabla de emisividades, parece que alumel (una aleación de níquel, aluminio, manganeso y silicio) funcionaría.
Lectura adicional:
Coeficientes de transferencia de calor por convección y radiación para segmentos individuales del cuerpo humano
Las influencias relativas de la radiación y la convección en la regulación de la temperatura del cuerpo vestido