El autobús experimenta una resistencia considerable y, por lo tanto, caerá más lentamente que una persona dentro del autobús. El escenario es posible en principio, pero después de ver cuidadosamente el clip y hacer algunos cálculos, creo que los detalles son inexactos.

Suponga que el autobús tiene una masa de 5000 kg (bastante ligero para un autobús), y tiene 3 m de ancho por 3 m de alto, por lo que el área orientada hacia adelante es de 9 m ² (será más si el autobús cae en ángulo, pero en la película parece que cae en línea recta. ¡A pesar del momento angular inicial cuando se vuelca!).

La fuerza de arrastre es

$$ F = \ frac12 \ rho v ^ 2 A C_D $$

Para las dimensiones dadas, después de un segundo la velocidad es de 5 m / sy esta fuerza será aproximadamente

$$ F (1) \ approx 0.5 \ cdot 1.2 \ cdot 5 ^ 2 \ cdot 9 \ cdot 1.15 = 135 N $$

(asumiendo un coeficiente de arrastre de 1 - cercano, pero un poco menor que, el coeficiente de un cubo; eso todavía no es suficiente para hacer que el autobús vaya visiblemente más lento.

Necesitamos saber qué tan alto es el puente. Resulta que esta escena se filmó en Lion's Gate Bridge en Vancouver. Th Tiene una altura libre de 61 m. Eso es más o menos lo que habría estimado en función de esta imagen (captura de pantalla del clip de YouTube a la 1:11, con bloques agregados por mí para mostrar que tiene aproximadamente 6 autobuses de altura. Un autobús típico mide aproximadamente 10 m de largo, por lo que todo tiene sentido ):

Ahora la caída real toma de 1:10 a 1:20 en el clip, lo que sugeriría que se está produciendo una "dilatación temporal". Normalmente, bajar 60 m tomaría 3.50 s; pero en la película se necesitan 10. Esta es una pista de que las leyes físicas normales se han suspendido para la escena.

Para un objeto en caída libre en presencia de resistencia, la velocidad terminal está dada por

$$ v_t = \ sqrt {\ frac {2mg} {C_D \ rho A}} $$

(Aproximadamente 95 m / s para este bus) y el "tiempo característico" $ \ tau $ (utilizado para la ecuación de movimiento)

$$ \ tau = \ frac {v_t} {g} $$

La velocidad en función de la altura es

$$ v = v_t \ sqrt {1-e ^ {- 2gh / v_t ^ 2}} $$

Esto significa que podemos calcular la velocidad del autobús y el pasajero en función de altura / tiempo: trazar su velocidad relativa y la posición del pasajero en relación con el autobús da:

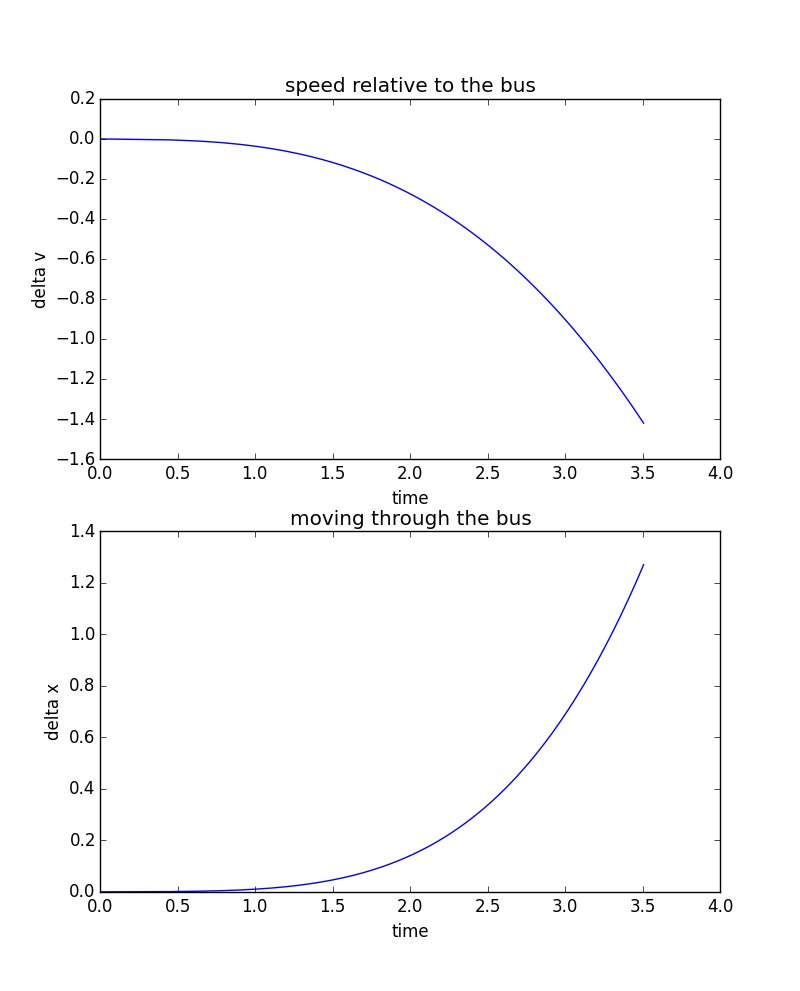
Esto me dice que la escena como se muestra en la película no siga la física newtoniana habitual. O el aire era ridículamente denso, el autobús era mucho más liviano de lo que parecía, o ... simplemente hicieron lo que querían porque eso es lo que pedía el guión. Física de películas.

Mito. Busted.

Si el autobús estuviera en el vacío (tanto dentro como fuera), el pasajero flotaría. Sin embargo, los efectos de la resistencia del aire en los dos objetos (pasajero y autobús) probablemente no sean despreciables en tal caso. El autobús se moverá en relación con el aire exterior y, por lo tanto, acelerará hacia el suelo a una velocidad inferior a $ g $. Si luego lanzamos un objeto dentro del autobús, desde el reposo con respecto al autobús, inicialmente acelerará hacia el suelo en $ g $ (ya que no hay resistencia del aire sobre él). Por lo tanto, el objeto se aceleraría hacia el suelo en una tarifa $ g $, y por lo tanto se movería hacia la parte delantera del autobús.

Efectivamente, la aceleración del autobús será $ \ vec {A} = \ vec {g} + \ vec {A} _ \ text {air} $, donde $ \ vec {A} _ \ text {air} $ es la aceleración del autobús debido a la resistencia del aire. (Tenga en cuenta que este último vector apunta hacia arriba). Un objeto de masa $ m $ en este marco de referencia no inercial obedecerá una versión de la ley de Newton que es algo así como $$ m \ vec {a} = m \ vec {g} + \ vec {F} _ \ text {aire} - m \ vec {A} = \ vec {F} _ \ text {aire} - m \ vec {A} _ \ text {aire}. $$ donde $ \ vec {a} $ es la aceleración del objeto relativa al autobús y $ \ vec {F} _ \ text {air} $ es ahora la fuerza de resistencia del aire sobre el objeto. Por lo tanto, vemos que inicialmente la aceleración será en la dirección opuesta a $ \ vec {A} $ (es decir, hacia abajo). Si el objeto pudiera caer lo suficiente en relación con el autobús, eventualmente alcanzaría su propia velocidad terminal en relación con el aire en el autobús; pero aún estaría cayendo en la dirección descendente en relación con el autobús.

Por último, tenga en cuenta que en el límite donde el autobús está cayendo a la velocidad terminal, los efectos de la resistencia del aire y la gravedad serían como los en el suelo, ya que el autobús se movería con velocidad constante. Por lo tanto, los objetos dentro del autobús se moverían (en relación con el autobús) tal como lo harían si el autobús estuviera apoyado en la tierra.

Oh, y toda esta derivación ignora cosas como la rotación del bus; un pasajero en un autobús que cae de un extremo a otro sentiría una fuerza centrífuga alejándose del centro de masa del autobús, incluso en ausencia de resistencia del aire. Pero esa es otra olla de pescado que no tengo tiempo de abrir en este momento.

Al principio, el autobús y la persona aceleraban al mismo ritmo debido a la gravedad. Sin embargo, la situación es más complicada debido a la resistencia del aire. El autobús experimenta resistencia al aire cuando cae. La persona dentro del autobús experimenta menos resistencia al aire porque el aire dentro del autobús se mueve con el autobús. Esto significa que la persona no experimenta tanta resistencia ya que no se mueve muy rápido con respecto al aire a su alrededor en el autobús.

Para poner números concretos en la situación, digamos que el autobús se está moviendo. a 80 millas / hora cuando golpea el agua. Eso significa que se enfrenta a un viento en contra de 80 millas / hora mientras cae, lo que ralentiza su aceleración. La persona que está adentro no experimenta este viento en contra porque el aire a su alrededor se mueve con el autobús (similar a cómo es más fácil nadar rápido en un río si se dirige río abajo). De este modo, puede alcanzar la parte delantera del autobús. Bueno, posiblemente. Eso dependería de la complicada aerodinámica del autobús y de la longitud de la caída. Pero, la película es al menos aproximadamente correcta.

No, no, ustedes (excepto Floris y los que lo votaron a favor) se perdieron una observación importante ... Miren con atención el video nuevamente.

Al principio, el autobús simplemente se inclina como el puente enfermedad de buzo. Cuando el autobús comienza a inclinarse (debido a la fricción con el puente aún no ha comenzado a caer) aún no ha obtenido una velocidad vertical considerable. Sin embargo, cuando el hombre pierde el equilibrio (si no hubiera sido una película, el hombre podría haberse sentado en un asiento para evitarlo), obtiene una pequeña velocidad vertical. Ahora que el autobús comienza a caer, ambos experimentan casi la misma aceleración (la diferencia debida a la resistencia del aire será inferior al 0,1% y no se notará a velocidades tan pequeñas y, obviamente, no puede otorgar una velocidad tan grande al hombre). Sin embargo, debido a la velocidad relativa inicial del hombre, sigue cayendo.

Si hubiera sido el caso de la resistencia del aire, se habría producido la siguiente observación: Conduzca un automóvil y obtenga una velocidad de aproximadamente 80 km / h. Ahora suelte el acelerador (NO presione los frenos). Debido a la resistencia del aire, el automóvil debería experimentar una fuerza hacia atrás que deberíamos experimentar tanta velocidad relativa como la experimentó el hombre de la película. Cualquier cosa que experimentemos se debe a la articulación del arrastre del aire y la fricción, pero aún así no se compararía con la velocidad que se muestra allí. Sin embargo, tome un soporte de gato y levante el automóvil para (no mucho) decir $ 30 ^ \ circ $ y siéntese en él (tenga en cuenta que en la película el automóvil se había inclinado más de $ 60 ^ \ circ $ antes de caer). Después de realizar estos dos experimentos (puedo imaginar el resultado sin siquiera experimentar) sabría cuál es la razón principal.

En primer lugar estudiemos un sistema imaginario en el que tanto el autobús como la persona no están sujetos a fuerzas de arrastre debidas al aire: si la persona no está atada a nada estará sujeta a caída libre y por lo tanto a una aceleración uniforme $ g $. Además, el autobús caerá libremente y, por lo tanto, caerán juntos con la misma velocidad.

Si tenemos en cuenta las fuerzas de arrastre:

Si el autobús y la persona caen por separado y ninguno de ellos tiene tiempo para alcanzar la velocidad terminal Argumento que la desaceleración debida a las fuerzas de arrastre es mayor en el autobús que en la persona (porque depende del tamaño de la proyección del objeto en el plano perpendicular a la velocidad y no sobre la masa del objeto) y luego diría que la persona "caería dentro del autobús".

En el mundo real, el aire dentro del autobús probablemente está cayendo junto con el autobús y, por lo tanto, diría que la fuerza de arrastre sobre la persona dentro del autobús es aún menor.