La eficiencia de un generador termoeléctrico es de alrededor del 5 al 8%.

La eficiencia de una gran central eléctrica de turbina de vapor se acerca al 40%.

De hecho, la eficiencia termodinámica de una gran planta de energía con turbina de vapor es superior al 90%, por lo que es tan eficiente como cualquier otra cosa. La máxima eficiencia posible de una máquina de vapor viene dada por el modelo idealizado llamado motor Carnot. En última instancia, la eficiencia está limitada por la diferencia de temperatura de los extremos frío y caliente del motor, y las plantas de energía modernas se acercan bastante a este máximo teórico.

Los generadores termoeléctricos tienden a usarse solo donde exigen otras restricciones su uso. Por ejemplo, el rover Curiousity utiliza un generador termoeléctrico con una eficiencia de aproximadamente el 6%. La menor eficiencia se compensa con la falta de partes móviles y, por supuesto, la falta de disponibilidad de agua en Marte para producir vapor.

mi pregunta es sobre si es posible en principio

La respuesta es sí 0000-.

y si cualquiera lo ha probado.

La respuesta es, por casualidad, no 0000-.

Entonces, ¿cómo es eso?

El efecto

El efecto termoeléctrico para la generación de electricidad (llamado efecto Seebeck ) es el fenómeno de que se genera un voltaje a una temperatura diferente en los extremos de un conductor:

$$ V = S \ Delta T $$

donde $ S $ es el coeficiente de Seebeck, una propiedad material. Todo lo que necesitamos es una diferencia de temperatura, es decir, una fuente caliente y una fría. Dicho en otras palabras, cualquier fuente caliente y cualquier fuente fría. Así que seguro, si tiene una fuente caliente que ciertamente es nuclear, y enfriamiento por agua, que es un método habitual para las centrales nucleares, solo necesita un material que tenga buenas propiedades en este rango de temperatura.

Los materiales

Pero aquí viene el problema. La búsqueda e investigación de materiales termoeléctricos es el freno en este campo. Simplemente no tenemos materiales suficientemente buenos en este momento. El tema todavía se siente nuevo, aunque se descubrió hace algunos cientos de años, y los mejores materiales en la actualidad siguen siendo los que se encontraron en la década de 1950. Estamos mejorando y mejorando, pero las eficiencias son simplemente demasiado bajas en comparación con cualquier otra fuente.

Eficiencia

No conozco la eficiencia típica de un Planta de energía nuclear. Pero un motor diésel, como ejemplo, tiene aproximadamente un 40% y es uno de los motores prácticos más eficientes que existen y que se utilizan en la actualidad.

Ahora, la máxima eficiencia de los dispositivos termoeléctricos es dado como:

$$ \ mu_ {max} = \ frac {T_C-T_H} {T_H} \ cdot \ frac {\ sqrt {1 + ZT} -1} {\ sqrt {1 + ZT } + T_H / T_C} = \ mu_ {Carnot} \ cdot \ mu_ {r} $$

donde $ T_H $ y $ T_C $ son temperaturas finales frías y calientes, y la eficiencia de Carnot es $ \ mu_ {Carnot} = \ frac {T_C-T_H} {T_H} $. El $ \ mu_r $, llamado eficiencia reducida o eficiencia de conversión , tal vez sea realista en alrededor de $ 10 \% $, mientras que el Carnot podría estar en quizás $ 60 \% $ - multiplíquelos juntos, y la eficiencia máxima $ \ mu_ {max} $ es simplemente demasiado baja.

Figura de mérito

Todo se reduce al la llamada figura de mérito $ ZT $, dada como:

$$ ZT = \ frac {S ^ 2 \ sigma} {\ kappa} $$

Para los materiales actuales del estado de la técnica, es solo de 1 a 1½. Yo mismo estoy trabajando con la aleación de telururo de bismuto, el mejor material en este momento en el rango de temperatura más bajo alrededor de la temperatura ambiente a 100-200 grados C, de los cuales el $ zT $ más alto alcanzado es $ zT \ sim 1.45 $ Se suele indicar que necesita alcanzar alrededor de 3-4 para que un material sea utilizable en la industria. Vea el gráfico de $ \ mu_r $ a continuación que muestra el valor de diferentes $ ZT $ s a diferentes temperaturas.

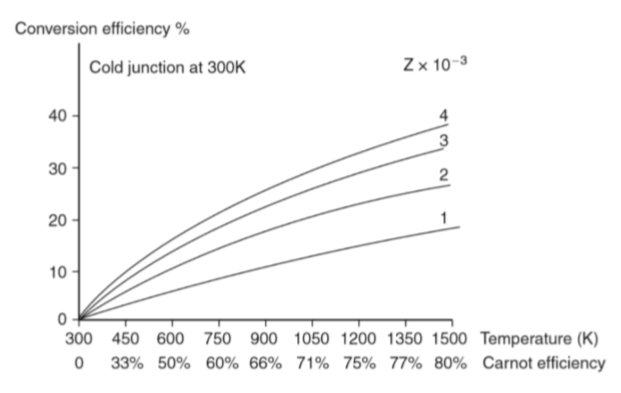
Fuente: Rowe, DM: " Manual Termoeléctrico - Macro a nano ”, Taylor & Francis Group, 2006.

El problema es principalmente la cuestión de reducir la conductividad térmica $ \ kappa $. Esto es principalmente ciencia material y un problema material que tenemos que superar, pero estoy totalmente de acuerdo en que este fenómeno físico debe tener un potencial enorme en algún momento.

Entonces, no sé si alguien alguna vez intentó poner en una planta de energía nuclear. Pero realmente no lo creo. Siempre que se encuentren mejores materiales, se necesitarán años para que se integren en plantas a gran escala.

En principio, la caída de la energía de Gibbs cuando el uranio se convierte en productos de fisión está disponible para realizar un trabajo útil. Si bien una máquina de vapor no se acercará a la máxima eficiencia posible alcanzable (que está muy cerca del 100%), un dispositivo termoeléctrico tendrá un rendimiento mucho peor, como se señala en detalle en las otras respuestas. La única manera de acercarse realmente a la eficiencia teórica de casi el 100% es utilizar la energía cinética de los productos de fisión directamente, en lugar de capturar la energía que resulta de que esa energía cinética se disipa primero en calor.

Sí, la gente usa termoeléctricos como parte de sistemas de generación de energía nuclear a muy pequeña escala, principalmente en naves espaciales: consulte Generador termoeléctrico de radioisótopos.

La gente normalmente no los llama cosas "plantas de energía nuclear ", pero definitivamente son un tipo de generación de energía nuclear.

Lockheed Martin fabrica un LH3 y LH8 que son generadores de energía nuclear termoeléctricos. Puedes por nuevo o usado. Tienes que conseguir el combustible del DoE o de los rusos.